■■ 遠隔地からロケット打ち上げを見る ■■
H3TF2 2024-02-17 09:22:55リフトオフ 546km離れた岡山県高梁市より
H3TF1 2023-03-07 10:37:55リフトオフ 400km離れた高知県須崎市より
他にも昼間の打ち上げを含む動画などをいくつかYoutubeで公開しているので結果だけ見てみたい場合は以下のリンクからアクセスしてみてほしい。
2018-01-18明け方のイプシロン3号機南打ちを岡山県高梁市よりみたところ
2017/08/11に予定されたH-IIA・F35の打ち上げの予定時間帯は14時頃~23時頃と発表されている。状況によっては夜間の打ち上げになる可能性もゼロではない。となれば本州からも見える可能性があるので準備だけはしておきたい。
液体燃料ロケットの場合ノズルの後ろから見る形でないとあまり明るく見えないという話を何処かで見た記憶もあるがこればかりは当日にならないとわからないだろう。肉眼で見えていなくても写真にはよく写る場合もあるので撮影の準備もしておきたい。となると、写野の中の飛行経路をシミュレートしておくことが必要になる。
打ち上げによっては公開されていないこともあるが、公開されている場合は「打上げ計画書」でググると手がかりとなるPDF資料が見つかる。例えば...
http://www.jaxa.jp/press/2017/06/files/20170615_h2af35_j.pdf
JAXA打上げ計画書より概要

これをみると自分の場所からの方位角と仰角が出せるので大体の見え方は予想でき、例えばここ岡山からだと20度位まで上るので、南西から南にかけて見晴らしのいい場所に陣取れば肉眼でも見える可能性がゼロではない。(固体燃料ロケットであるイプシロン2の夜間打ち上げはよく見えた。)
JAXAが公開する打ち上げ計画書に出ている地図上の位置と計画表の経過時間・高度を紙にプロットしてやれば大体の飛行経路はわかるがPCを使えば便利に処理できる。ここで強い味方になるのがGoogleEarth。そしてロケットの飛行経路を個人的に計算してKMLを公開してくださっている「ロケッこ」様のサイト「ロケッこがゆく」である。
H-IIA F35 みちびき3号~見え方予想
液体燃料ロケットの場合ノズルの後ろから見る形でないとあまり明るく見えないという話を何処かで見た記憶もあるがこればかりは当日にならないとわからないだろう。肉眼で見えていなくても写真にはよく写る場合もあるので撮影の準備もしておきたい。となると、写野の中の飛行経路をシミュレートしておくことが必要になる。
打ち上げによっては公開されていないこともあるが、公開されている場合は「打上げ計画書」でググると手がかりとなるPDF資料が見つかる。例えば...
http://www.jaxa.jp/press/2017/06/files/20170615_h2af35_j.pdf
JAXA打上げ計画書より概要
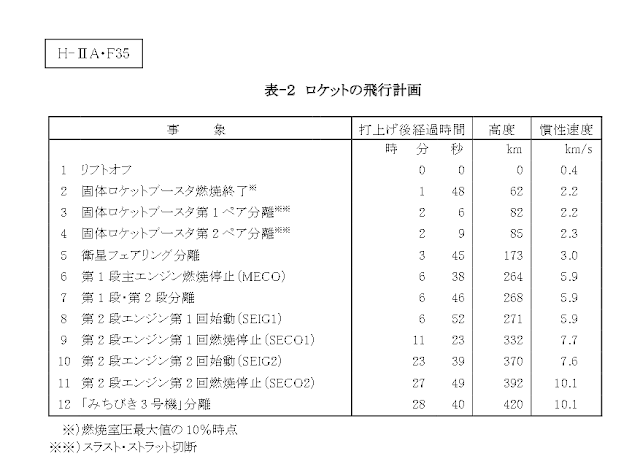
H-IIA・F35は、「みちびき3号機」を搭載し種子島宇宙センター大型ロケット第1射点より打ち上げられる。ロケットは、打上げ後まもなく機体のピッチ面を方位角92.5度へ向けた後、表-2に示す所定の飛行計画に従って太平洋上を飛行する。打上げ約1分48秒後に固体ロケットブースタの燃焼を終了し、約2分6秒後及び約2分9秒後(以下、時間は打上げ後の経過時間を示す。)に分離する。衛星フェアリングを約3分45秒後に分離し、約6分38秒後には第1段主エンジンの燃焼を停止し、約6分46秒後に第1段を分離する。引き続いて、約6分52秒後に第2段エンジン第1回目の燃焼が開始され、約11分23秒後に燃焼を停止、慣性飛行を続けた後、約23分39秒後に第2段エンジン第2回目の燃焼を開始、約27分49秒後に燃焼を停止、約28分40秒後に近地点高度約380km、遠地点高度約35976km、軌道傾斜角20度の静止遷移軌道上で「みちびき3号機」を分離する。


これをみると自分の場所からの方位角と仰角が出せるので大体の見え方は予想でき、例えばここ岡山からだと20度位まで上るので、南西から南にかけて見晴らしのいい場所に陣取れば肉眼でも見える可能性がゼロではない。(固体燃料ロケットであるイプシロン2の夜間打ち上げはよく見えた。)
JAXAが公開する打ち上げ計画書に出ている地図上の位置と計画表の経過時間・高度を紙にプロットしてやれば大体の飛行経路はわかるがPCを使えば便利に処理できる。ここで強い味方になるのがGoogleEarth。そしてロケットの飛行経路を個人的に計算してKMLを公開してくださっている「ロケッこ」様のサイト「ロケッこがゆく」である。
H-IIA F35 みちびき3号~見え方予想
http://blog.syo-ko.com/?eid=2587
このページ内のマイマップ右上隅のアイコン「拡大地図を表示」をクリックすると左側に表示されるエリアの一番上、ルーペアイコンの右のドット3つのメニューから「KMLをダウンロード」を選択、チェックを入れずにダウンロードするとKMZファイルが落とせる。GoogleEarthの「ファイル」メニューから「開く」でこのKMZファイルを開けば経路のパス情報やポイントの情報が含まれている。この開き方でマイマップからGoogleEarthにインポートしたKMLは地面に貼り付いた形になっているのでオブジェクトごとに右クリックでプロパティを開き、標高タブの標高のところを「地面に固定」から「地面に相対」や「標高」に変更してやると高さ情報が復元される。
によるとFull Size DSLRの場合の水平画角は
16mm lens - 96.7° hFOV
このページ内のマイマップ右上隅のアイコン「拡大地図を表示」をクリックすると左側に表示されるエリアの一番上、ルーペアイコンの右のドット3つのメニューから「KMLをダウンロード」を選択、チェックを入れずにダウンロードするとKMZファイルが落とせる。GoogleEarthの「ファイル」メニューから「開く」でこのKMZファイルを開けば経路のパス情報やポイントの情報が含まれている。この開き方でマイマップからGoogleEarthにインポートしたKMLは地面に貼り付いた形になっているのでオブジェクトごとに右クリックでプロパティを開き、標高タブの標高のところを「地面に固定」から「地面に相対」や「標高」に変更してやると高さ情報が復元される。
KML(Keyhole Markup Language)については
https://developers.google.com/kml/documentation/?hl=ja 等を参照
KMZファイルはKMLファイルその他をZIPアーカイブしたものなので拡張子をzipに変更して解凍すればKMLファイルになりテキストエディタで開くことができる。詳しくは
https://developers.google.com/kml/documentation/kmzarchives?hl=ja
ロケッこ様のKMLでは飛行経路は一本で時刻情報は含まれていないので、ロケットの移動や、どの部分で光っていてどの部分で慣性飛行しているかがわかりやすいように少し手を加えて撮影の手助けになるデータを作ってみたがこれについては別記事にまとめたい。
また、無料になったGoogleEarthProを使えばロケットの動きや視点移動も含む「ツアー」の動画も作成できるので各地からどのように見えるかを動画でシミュレートすることも可能になる。デフォルトではHFOV(Horizontal FOV)は 60度くらいになっているらしい。
写真撮影をする場合は写野が気になるがGoogleEarthのGUIでFOV(Field Of View)を手軽に変更する方法は今のところ見当たらない。(FOVを変更するKMLを作成して開くことで可能)例えば
https://www.gearthblog.com/blog/archives/2015/03/google-maps-earth-view-fov.htmlhttps://en.wikipedia.org/wiki/Angle_of_view
によるとFull Size DSLRの場合の水平画角は
16mm lens - 96.7° hFOV
24mm lens - 73.7° hFOV
35mm lens - 54.4° hFOV
50mm lens - 39.6° hFOV
70mm lens - 28.8° hFOV
85mm lens - 23.9° hFOV
105mm lens - 19.5° hFOV
200mm lens - 10.3° hFOV
と、当時このあたりまで書いてはいたが結局ロケットは見えなかったため放置していた。
延期のため2020/02/09に変更されたH2AF41打ち上げに際して岡山県南にも晴れ間ができそうだったので昼間の打ち上げが見えるかどうかを確かめようと計画した。
supercweather.comの予測によると高梁方面はだめ、県南は雲が少なめだが打ち上げ時刻が近づくに連れて雲が多くなる予測。広島よりの方が雲が出ないようだったので視界の開けたポイントをGoogleEarthで探し回り福山市内海の海岸に遮る山が少なく予定時刻あたりで四国方面も雲が少ないという格好の場所を見つけていた。
ところが、当日車で出発するとタイヤの空気圧がおかしい。SSで空気を入れ足すと「しゅー」音が。前日は問題なかったのにどこで何を踏んだのだろう?タイヤを交換してもらい時間に余裕がなくなったので近場に変更。やはり雲が多め、特に四国山地が雲で覆われている。うーん残念。ただ四国山地の上にかかる雲よりも上は霞んではいるけれど一応晴れている状況。でノーマルのEOSと天体改造EOS6D+IR850nmフィルタとを試してみた。
結果の写真は後ろの方に貼ったが結論としては何も写せなかった。
330mm望遠+CMOSカメラも用意していたがタイヤ交換のため用意している余裕がなくなり次回の課題とした。
この時実感したのが観測場所ごとに精密な予測をしておくことの必要性である。
望遠で狙うには手前の山の端のどこから出てくるかが正確にわかっていないといけない。そして、見えないところから突然出現するものなので秒単位の時刻の予報が欠かせないと思った。この記事を書いている理由はここにある。
飛行コース、時刻、到達高度は与えられたが問題は地球の丸み。赤道の長さを4万キロ、倉敷ー種子島間を500キロとすると地球の中心から見た2地点間の角度はだいたい500/40000*360=4.5度となり無視できない気がする。射点が見えない遠隔地からロケットを見る場合に共通する課題と思われるのでもう少しちゃんと検討してみたい。
ところで、Mathematicaを生み出した天才Stephen Wolframが2009年に始めたWolframAlphaは森羅万象を計算してくれるすごいシステム。無償公開され進化を続けているが2018年には日本語版も開始された。
入力フィールドにとりあえず「地平線との距離」と入れてみる。
https://ja.wolframalpha.com/
答えは「Wolfram|Alphaは,このクエリが理解できません.」
残念、自然言語を翻訳するのは難しそう。
繋がっているのがいけないかもしれないのでスペースで区切って入れてみる。

日産スカイラインのホイールベースが出てきた。
これはこれですごいが...やはり使えないのか?
「水平線 距離」でもうまく行かなかったので英語で入力してみると...

おっ、標高を入力するダイアログと計算ボタンが出現したではないか!
計算ボタンを押すとたちどころに...

解説付きで答えが出た。デフォルトで入ってる数値(成人の視点の高さか?)で計算した地平線までの距離が4830mと出た。地平線までの距離って意外と近い。ゆっくり歩いても1時間(^^)。
d(Direct Horizon Distance)は地球中心・ロケット・観測点を結ぶ直角三角形を想定し三平方の定理を使えば、d^2+a^2=(a+h)^2 の関係から導けるのでルートの入った式はこれから出てきたものだろう。
今回は逆に観測場所とロケットとの距離(=ロケットから見える地平線までの距離)dを与えてロケットの高さhを求めたいので、hを変数にした2次方程式を解くことになる。2次方程式の公式に当てはめてもよいが、せっかくWolframAlphaを開いているので答えを聞いてみる。
上図の「方程式」フィールドをクリックするとプレーンテキストに変更するボタンが出るので押してみるとこの式をどうやって入力してやればよいかがわかる。
観測地とロケットの距離もWolframAlphaで確認する。

地球の半径a_earthは6378kmとすでに上に表示されているので
d = sqrt(h (h + 2 a_earth ))
にそのまま具体的な数値を代入すれば方程式ができる。
517=sqrt(h (h + 2 *6378 ))
この方程式をそのままWolframAlphaに貼り付けてみるとグラフや厳密解が表示され

「近似値」ボタンを押すと
h≈20.920 kmと出た。
つまり倉敷の海抜ゼロ地点から種子島を見ているとき、ロケットが標高21kmまで上昇して初めて地平線上に見え始めるということ。45km程度でSRB燃焼終了となっている打ち上げもあるのでこの数値は大きい。おいしい前半が絶対見えないというのは悔しい。
もちろんこれは真空中での話で、実際には大気の屈折により少し浮き上がって見えるので原理的にはこの計算よりもわずかに低い位置からロケットが見え始める。
見かけの高度が低いほど大気による浮き上がりが大きくなり、この量をWikipediaの「大気差」で確認してみると概算値が以下のようになっている。(温度を考慮した計算式もあるが大気の状態に依存するので厳密な値を出すのは難しい)
大気差の概略値
まあ、低空まで完全に透明度が完璧で雲も靄も皆無という気象条件は望めないので通常は大気差は無視できるのではないかと思われる。そもそも地平線水平線よりも手前に山があるので大気差については考慮しなくて良いだろう。
ちなみに、WolframAlphaでdをパラメータとしてhをグラフにすることもできる。
カノープスの北限に挑戦する人はこの大気差を考慮する必要があるだろう。
ここまでは標高ゼロメートルからロケットを見た場合の検討だったが、実際に遠くの高い位置にあるロケットをよく見たい場合は、直感的にこちらも標高の高い位置に移動したほうが有利と思われる。登山をする人は登るにつれて遠くの高い山(富士山とか)がまわりと比較してどんどんせり上がってくる経験があるのではないだろうか。
そこでときどき星見に出かける高梁市の見晴らしの良い場所(標高450メートル)から見た場合とを比較してみることにする。
ここでWolframAlphaではなくユーザー登録だけで無償で使えるWolfram言語環境を使ってみる。無償のBasicプランでも関数の実行やノートブック(作成したドキュメント)の保存ができる。
https://www.wolframcloud.com/
観測地の標高 h 定数 = 0.45km
ロケットの標高 H 変数
観測地BとロケットCを結ぶ線分がちょうど海抜ゼロの地表面に接する場所を基準点Aとする。
地球の半径をRとするとR = 6378km
「Distance Tanegashima Takahashi」
をWolframAlphaに入力して得た答えは 529.4 km
まず定数を代入しておき、3つの連立方程式から変数x,X,Hを求める。
厳密解は必要ないのでSolveでなくNSolveを使う。
h=0.45;
R=6378;
L=529.4;
NSolve[{
AB+AC==L,
(h+R)^2==AB^2+R^2,
(H+R)^2==AC^2+R^2,
AB>0,AC>0,H>0
}]
{{AB->75.7654,AC->453.635,H->16.112}}
倉敷を観測地とした場合ロケットが21kmまで上がってようやく地平線に見え始めるのに対して、高梁市の標高450mからはロケットが16km上がっただけで見え始めることがわかる。
また観測地から見た地平線までの距離は76km、ロケットからは454kmとなる。
AB,ACがわかったので正しい比率で作図してみる。
R=6378;
Show[Graphics[{
Circle[{0,-R},R,{Pi/2+1.1/180Pi,Pi/2-4.5/180Pi}],
Line[{{-75.7654,0},{0,-R},{453.635,0}}]},
{Axes->True,AxesStyle->RGBColor[1,0,0],
PlotRange->{{-100,510},{-100,10}},
Background->RGBColor[0.84,0.92,1.]}]]
高梁側がよくわかるようにPlotRangeを狭く指定して描画すると
PlotRangeの指定を削除してやると全体が表示される。地球中心の座標が(0,-R)
ロケットによっては高度45kmでSRB燃焼終了になるのでこの4キロの差は大きいかもしれない。打ち上げ直後のSRB燃焼やロケット雲が狙いの場合は低いうちから見えるほど有利。よって観測地および観測地から南西方面の天候さえ良ければとにかく高いところに陣取るのがよさそう。
h=0.55 に変更すると
{{x->83.7096,X->445.69,H->15.5728}}
近隣2箇所にこの標高の場所があるので下見をしておきたいと思っている。GoogleEarthではStreetViewが訪問していない場所でもレンダリングできるので遠方についてはOKだが、現地の状況はやはり訪問しないとわからない。
と、当時このあたりまで書いてはいたが結局ロケットは見えなかったため放置していた。
延期のため2020/02/09に変更されたH2AF41打ち上げに際して岡山県南にも晴れ間ができそうだったので昼間の打ち上げが見えるかどうかを確かめようと計画した。
supercweather.comの予測によると高梁方面はだめ、県南は雲が少なめだが打ち上げ時刻が近づくに連れて雲が多くなる予測。広島よりの方が雲が出ないようだったので視界の開けたポイントをGoogleEarthで探し回り福山市内海の海岸に遮る山が少なく予定時刻あたりで四国方面も雲が少ないという格好の場所を見つけていた。
ところが、当日車で出発するとタイヤの空気圧がおかしい。SSで空気を入れ足すと「しゅー」音が。前日は問題なかったのにどこで何を踏んだのだろう?タイヤを交換してもらい時間に余裕がなくなったので近場に変更。やはり雲が多め、特に四国山地が雲で覆われている。うーん残念。ただ四国山地の上にかかる雲よりも上は霞んではいるけれど一応晴れている状況。でノーマルのEOSと天体改造EOS6D+IR850nmフィルタとを試してみた。
結果の写真は後ろの方に貼ったが結論としては何も写せなかった。
330mm望遠+CMOSカメラも用意していたがタイヤ交換のため用意している余裕がなくなり次回の課題とした。
この時実感したのが観測場所ごとに精密な予測をしておくことの必要性である。
望遠で狙うには手前の山の端のどこから出てくるかが正確にわかっていないといけない。そして、見えないところから突然出現するものなので秒単位の時刻の予報が欠かせないと思った。この記事を書いている理由はここにある。
■■ 地球は丸かった。 ■■
飛行コース、時刻、到達高度は与えられたが問題は地球の丸み。赤道の長さを4万キロ、倉敷ー種子島間を500キロとすると地球の中心から見た2地点間の角度はだいたい500/40000*360=4.5度となり無視できない気がする。射点が見えない遠隔地からロケットを見る場合に共通する課題と思われるのでもう少しちゃんと検討してみたい。
ところで、Mathematicaを生み出した天才Stephen Wolframが2009年に始めたWolframAlphaは森羅万象を計算してくれるすごいシステム。無償公開され進化を続けているが2018年には日本語版も開始された。
入力フィールドにとりあえず「地平線との距離」と入れてみる。
https://ja.wolframalpha.com/
答えは「Wolfram|Alphaは,このクエリが理解できません.」
残念、自然言語を翻訳するのは難しそう。
繋がっているのがいけないかもしれないのでスペースで区切って入れてみる。

日産スカイラインのホイールベースが出てきた。
これはこれですごいが...やはり使えないのか?
「水平線 距離」でもうまく行かなかったので英語で入力してみると...

おっ、標高を入力するダイアログと計算ボタンが出現したではないか!
計算ボタンを押すとたちどころに...

解説付きで答えが出た。デフォルトで入ってる数値(成人の視点の高さか?)で計算した地平線までの距離が4830mと出た。地平線までの距離って意外と近い。ゆっくり歩いても1時間(^^)。
d(Direct Horizon Distance)は地球中心・ロケット・観測点を結ぶ直角三角形を想定し三平方の定理を使えば、d^2+a^2=(a+h)^2 の関係から導けるのでルートの入った式はこれから出てきたものだろう。
今回は逆に観測場所とロケットとの距離(=ロケットから見える地平線までの距離)dを与えてロケットの高さhを求めたいので、hを変数にした2次方程式を解くことになる。2次方程式の公式に当てはめてもよいが、せっかくWolframAlphaを開いているので答えを聞いてみる。
上図の「方程式」フィールドをクリックするとプレーンテキストに変更するボタンが出るので押してみるとこの式をどうやって入力してやればよいかがわかる。
d = sqrt(h (h + 2 a_earth )) | s = a_earth sec^(-1)(1 + h/a_earth ) |d | direct horizon distanceh | altitudes | horizon distance along surfacea_ earth | Earth equatorial radius (≈ 6.378×10^6 m)(ignoring topography and other obstructions)
観測地とロケットの距離もWolframAlphaで確認する。

地球の半径a_earthは6378kmとすでに上に表示されているので
d = sqrt(h (h + 2 a_earth ))
にそのまま具体的な数値を代入すれば方程式ができる。
517=sqrt(h (h + 2 *6378 ))
この方程式をそのままWolframAlphaに貼り付けてみるとグラフや厳密解が表示され

「近似値」ボタンを押すと
h≈20.920 kmと出た。
つまり倉敷の海抜ゼロ地点から種子島を見ているとき、ロケットが標高21kmまで上昇して初めて地平線上に見え始めるということ。45km程度でSRB燃焼終了となっている打ち上げもあるのでこの数値は大きい。おいしい前半が絶対見えないというのは悔しい。
もちろんこれは真空中での話で、実際には大気の屈折により少し浮き上がって見えるので原理的にはこの計算よりもわずかに低い位置からロケットが見え始める。
見かけの高度が低いほど大気による浮き上がりが大きくなり、この量をWikipediaの「大気差」で確認してみると概算値が以下のようになっている。(温度を考慮した計算式もあるが大気の状態に依存するので厳密な値を出すのは難しい)
大気差の概略値
視高度 大気差
0° 34’20”
5° 9’50”
10° 5’
20° 2’40”
30° 1’40”
45° 1’
60° 0’30”
まあ、低空まで完全に透明度が完璧で雲も靄も皆無という気象条件は望めないので通常は大気差は無視できるのではないかと思われる。そもそも地平線水平線よりも手前に山があるので大気差については考慮しなくて良いだろう。
ちなみに、WolframAlphaでdをパラメータとしてhをグラフにすることもできる。
カノープスの北限に挑戦する人はこの大気差を考慮する必要があるだろう。
■■ 高いところに登ったらどうか? ■■
ここまでは標高ゼロメートルからロケットを見た場合の検討だったが、実際に遠くの高い位置にあるロケットをよく見たい場合は、直感的にこちらも標高の高い位置に移動したほうが有利と思われる。登山をする人は登るにつれて遠くの高い山(富士山とか)がまわりと比較してどんどんせり上がってくる経験があるのではないだろうか。
そこでときどき星見に出かける高梁市の見晴らしの良い場所(標高450メートル)から見た場合とを比較してみることにする。
ここでWolframAlphaではなくユーザー登録だけで無償で使えるWolfram言語環境を使ってみる。無償のBasicプランでも関数の実行やノートブック(作成したドキュメント)の保存ができる。
https://www.wolframcloud.com/
観測地の標高 h 定数 = 0.45km
ロケットの標高 H 変数
観測地BとロケットCを結ぶ線分がちょうど海抜ゼロの地表面に接する場所を基準点Aとする。
地球の半径をRとするとR = 6378km
「Distance Tanegashima Takahashi」
をWolframAlphaに入力して得た答えは 529.4 km
まず定数を代入しておき、3つの連立方程式から変数x,X,Hを求める。
厳密解は必要ないのでSolveでなくNSolveを使う。
h=0.45;
R=6378;
L=529.4;
NSolve[{
AB+AC==L,
(h+R)^2==AB^2+R^2,
(H+R)^2==AC^2+R^2,
AB>0,AC>0,H>0
}]
{{AB->75.7654,AC->453.635,H->16.112}}
倉敷を観測地とした場合ロケットが21kmまで上がってようやく地平線に見え始めるのに対して、高梁市の標高450mからはロケットが16km上がっただけで見え始めることがわかる。
また観測地から見た地平線までの距離は76km、ロケットからは454kmとなる。
AB,ACがわかったので正しい比率で作図してみる。
R=6378;
Show[Graphics[{
Circle[{0,-R},R,{Pi/2+1.1/180Pi,Pi/2-4.5/180Pi}],
Line[{{-75.7654,0},{0,-R},{453.635,0}}]},
{Axes->True,AxesStyle->RGBColor[1,0,0],
PlotRange->{{-100,510},{-100,10}},
Background->RGBColor[0.84,0.92,1.]}]]
高梁側がよくわかるようにPlotRangeを狭く指定して描画すると

PlotRangeの指定を削除してやると全体が表示される。地球中心の座標が(0,-R)
ロケットによっては高度45kmでSRB燃焼終了になるのでこの4キロの差は大きいかもしれない。打ち上げ直後のSRB燃焼やロケット雲が狙いの場合は低いうちから見えるほど有利。よって観測地および観測地から南西方面の天候さえ良ければとにかく高いところに陣取るのがよさそう。
h=0.55 に変更すると
{{x->83.7096,X->445.69,H->15.5728}}
近隣2箇所にこの標高の場所があるので下見をしておきたいと思っている。GoogleEarthではStreetViewが訪問していない場所でもレンダリングできるので遠方についてはOKだが、現地の状況はやはり訪問しないとわからない。
なお、実は代入のところを手作業で置き換えれば、この連立方程式をWolframAlphaに与えて解くことも可能。まあでもWolframCloudの方が色々自由にできて楽しいのでこちらをおすすめする。

ここでも引き続き https://www.wolframcloud.com/ を使うことにする。
前提条件として計画書に載っている以下の値を使う。
検討するのは主モータとSRBが燃焼している間なのでこの両端の質量がわかれば加速度の比がわかり、これから2.2km/sに達するまでの速度プロファイル、ひいては62kmに達するまでの高度プロファイルもわかると思われる。
打ち上げの瞬間は垂直でその後ノズルの方向を動かして東向きに変針しているはずだが
ロケットの構成や燃料の質量はWikipediaの「H-IIAロケット」
Wikipediaで確認するとH2AF35の場合型式名はH2A204型と呼ばれるもので諸元は以下の通り
全体質量445t
→お客さんである「みちびき3」は含まれないかもしれないので4.7tを加えて総質量450tとする。
SRBの燃料は66t x4本
主モータの燃料は101tだが390秒のうち108秒までに消費するのは101x108/390=28tとしておくと
108秒後には総質量=450-66x4-28=158tとなる。
したがって打ち上げ時と燃焼終了時では加速度の比率は
158:450=1:2.848となる。
In[1]:= atemp = t/108*1.848+1
Out[1]= 1+0.0171111 t
速度をvとすると
In[2]:= v = atemp t
Out[2]= (1+0.0171111 t) t
atempは仮の値であり、このままでは終端が2.2km/sにならないので、
In[3]:= vtemp = v /. {t -> 108}
Out[3]= 307.584
In[4]:= v = atemp t*2200/vtemp
Out[4]= 7.15252 (1 + 0.0171111 t) t
調整後の本当の加速度は
In[ ]:= a = D[v,t]//Simplify
Out[ ]= 7.15252 + 0.244775 t
単位をGで表すには9.8m/s2で割って
In[ ]:= g = a/9.8;
確認のためこれらをプロットしてみる。
加速度
この式hkmが定まると目視可能になる標高に達する時刻がわかるようになる。
In[10]:= Solve[{hkm==21,t>0}]
Out[10]= {{t->70.017}}
例えば先に求めた21kmまで上昇するのは打ち上げ後70秒とわかる。
In[11]:= Solve[{hkm==16,t>0}]
Out[11]= {{t->62.605}}
16kmまで上昇するのは打ち上げ後63秒
都度Solveするのは面倒なので数表を作っておこう。
時刻の数列を1秒刻みにt0とすると
In[12]:= t0=Range[109]-1
Out[12]= {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,
22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,
44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,
66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,
88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,
107,108}
これを先ほど求めたhkmに代入する。
In[13]:= ht=0.00476299 (0.5 t^2 + 0.0057037 t^3) /.{t->t0}
Out[13]= {0.,0.00240866,0.00974331,0.022167,0.0398426,0.0629332,
0.0916018,0.126011,0.166325,0.212706,0.265316,0.32432,0.389879,
0.462158,0.541318,0.627524,0.720937,0.821722,0.93004,1.04606,
1.16993,1.30183,1.44191,1.59035,1.74729,1.91291,2.08737,2.27083,
2.46345,2.66541,2.87685,3.09794,3.32885,3.56974,3.82077,4.0821,
4.35391,4.63634,4.92957,5.23375,5.54906,5.87565,6.21368,6.56332,
6.92474,7.29809,7.68354,8.08125,8.49138,8.9141,9.34957,9.79795,
10.2594,10.7341,11.2222,11.7239,12.2393,12.7686,13.3119,13.8694,
14.4414,15.0279,15.629,16.2451,16.8762,17.5225,18.1841,18.8613,
19.5541,20.2628,20.9875,21.7284,22.4856,23.2593,24.0497,24.8568,
25.681,26.5224,27.381,28.2571,29.1509,30.0625,30.992,31.9397,
32.9056,33.89,34.8931,35.9149,36.9556,38.0155,39.0946,40.1932,
41.3113,42.4492,43.6071,44.785,45.9832,47.2018,48.4409,49.7008,
50.9816,52.2835,53.6066,54.951,56.3171,57.7048,59.1144,60.5461,
61.9999}
ついでに速度も
In[14]:= vt=0.00715252 (1 + 0.0171111 t) t /.{t->t0}
Out[14]= {0.,0.00727491,0.0147946,0.022559,0.0305683,0.0388223,
0.0473211,0.0560646,0.065053,0.0742861,0.0837639,0.0934866,
0.103454,0.113666,0.124123,0.134825,0.145772,0.156963,0.168399,
0.18008,0.192005,0.204176,0.216591,0.229251,0.242156,0.255305,
0.268699,0.282339,0.296222,0.310351,0.324724,0.339342,0.354205,
0.369313,0.384666,0.400263,0.416105,0.432192,0.448523,0.4651,
0.481921,0.498987,0.516297,0.533853,0.551653,0.569698,0.587988,
0.606522,0.625302,0.644326,0.663595,0.683108,0.702867,0.72287,
0.743118,0.763611,0.784348,0.805331,0.826558,0.84803,0.869746,
0.891708,0.913914,0.936365,0.95906,0.982001,1.00519,1.02862,
1.05229,1.07621,1.10038,1.12478,1.14944,1.17434,1.19948,1.22487,
1.2505,1.27638,1.3025,1.32887,1.35548,1.38234,1.40944,1.43679,
1.46438,1.49221,1.52029,1.54862,1.57719,1.60601,1.63507,1.66437,
1.69392,1.72371,1.75375,1.78404,1.81456,1.84534,1.87636,1.90762,
1.93913,1.97088,2.00288,2.03512,2.06761,2.10034,2.13331,2.16653,
2.2}
時速km/sもついでに
In[15]:= vtkmph=Round[vt*60*60]
Out[15]= {0,26,53,81,110,140,170,202,234,267,302,337,372,409,447,
485,525,565,606,648,691,735,780,825,872,919,967,1016,1066,1117,
1169,1222,1275,1330,1385,1441,1498,1556,1615,1674,1735,1796,1859,
1922,1986,2051,2117,2183,2251,2320,2389,2459,2530,2602,2675,2749,
2824,2899,2976,3053,3131,3210,3290,3371,3453,3535,3619,3703,3788,
3874,3961,4049,4138,4228,4318,4410,4502,4595,4689,4784,4880,4976,
5074,5172,5272,5372,5473,5575,5678,5782,5886,5992,6098,6205,6314,
6423,6532,6643,6755,6867,6981,7095,7210,7326,7443,7561,7680,7800,
7920}
APL言語みたいでとてもお手軽である。
これらをt0と並べると4行109列のArrayになる。
In[16]:= {t0,ht,vt,vtkmph}
Out[16]= {{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,
21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,
42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,
63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,
84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,
104,105,106,107,108},{0.,0.00240866,0.00974331,0.022167,
0.0398426,0.0629332,0.0916018,0.126011,0.166325,0.212706,
0.265316,0.32432,0.389879,0.462158,0.541318,0.627524,0.720937,
0.821722,0.93004,1.04606,1.16993,1.30183,1.44191,1.59035,1.74729,
1.91291,2.08737,2.27083,2.46345,2.66541,2.87685,3.09794,3.32885,
3.56974,3.82077,4.0821,4.35391,4.63634,4.92957,5.23375,5.54906,
5.87565,6.21368,6.56332,6.92474,7.29809,7.68354,8.08125,8.49138,
8.9141,9.34957,9.79795,10.2594,10.7341,11.2222,11.7239,12.2393,
12.7686,13.3119,13.8694,14.4414,15.0279,15.629,16.2451,16.8762,
17.5225,18.1841,18.8613,19.5541,20.2628,20.9875,21.7284,22.4856,
23.2593,24.0497,24.8568,25.681,26.5224,27.381,28.2571,29.1509,
30.0625,30.992,31.9397,32.9056,33.89,34.8931,35.9149,36.9556,
38.0155,39.0946,40.1932,41.3113,42.4492,43.6071,44.785,45.9832,
47.2018,48.4409,49.7008,50.9816,52.2835,53.6066,54.951,56.3171,
57.7048,59.1144,60.5461,61.9999},{0.,0.00727491,0.0147946,
0.022559,0.0305683,0.0388223,0.0473211,0.0560646,0.065053,
0.0742861,0.0837639,0.0934866,0.103454,0.113666,0.124123,
0.134825,0.145772,0.156963,0.168399,0.18008,0.192005,0.204176,
0.216591,0.229251,0.242156,0.255305,0.268699,0.282339,0.296222,
0.310351,0.324724,0.339342,0.354205,0.369313,0.384666,0.400263,
0.416105,0.432192,0.448523,0.4651,0.481921,0.498987,0.516297,
0.533853,0.551653,0.569698,0.587988,0.606522,0.625302,0.644326,
0.663595,0.683108,0.702867,0.72287,0.743118,0.763611,0.784348,
0.805331,0.826558,0.84803,0.869746,0.891708,0.913914,0.936365,
0.95906,0.982001,1.00519,1.02862,1.05229,1.07621,1.10038,
1.12478,1.14944,1.17434,1.19948,1.22487,1.2505,1.27638,1.3025,
1.32887,1.35548,1.38234,1.40944,1.43679,1.46438,1.49221,1.52029,
1.54862,1.57719,1.60601,1.63507,1.66437,1.69392,1.72371,1.75375,
1.78404,1.81456,1.84534,1.87636,1.90762,1.93913,1.97088,2.00288,
2.03512,2.06761,2.10034,2.13331,2.16653,2.2},{0,26,53,81,110,
140,170,202,234,267,302,337,372,409,447,485,525,565,606,648,691,
735,780,825,872,919,967,1016,1066,1117,1169,1222,1275,1330,1385,
1441,1498,1556,1615,1674,1735,1796,1859,1922,1986,2051,2117,
2183,2251,2320,2389,2459,2530,2602,2675,2749,2824,2899,2976,
3053,3131,3210,3290,3371,3453,3535,3619,3703,3788,3874,3961,
4049,4138,4228,4318,4410,4502,4595,4689,4784,4880,4976,5074,
5172,5272,5372,5473,5575,5678,5782,5886,5992,6098,6205,6314,
6423,6532,6643,6755,6867,6981,7095,7210,7326,7443,7561,7680,
7800,7920}}
Prepend関数でタイトルヘッダ文字列を連結し、転置する。
In[17]:= Prepend[Transpose[{t0,ht,vt,vtkmph}],
{"経過秒","高度km","速度km/s","速度km/h"}];
Short[%,10]
Out[17]= {{経過秒,高度km,速度km/s,速度km/h},{0,0.,0.,0},
{1,0.00240866,0.00727491,26},{2,0.00974331,0.0147946,53},
{3,0.022167,0.022559,81},{4,0.0398426,0.0305683,110},
<<98>>,{103,54.951,2.03512,7326},{104,56.3171,2.06761,7443},
{105,57.7048,2.10034,7561},{106,59.1144,2.13331,7680},
{107,60.5461,2.16653,7800},{108,61.9999,2.2,7920}}
枠をつけると数表ができた。
In[18]:= Grid[%,{Alignment->Left,Dividers->{All,All}}]
%というのは直前に評価した結果を表す。
In,Outの数字を使って%nnとすればnn番目の結果を表す。
これはグラフィックスのオブジェクトでも構わない。
入力のあと「;」をつければ結果は表示されない。
以上経過を確認しながら計算してきたが、;で区切りながら
一つのセルに入力しておき、そのセルにフォーカスがある状態で
Shift+Enterを押せば上の表が一発で返ってくることになる。
tmax = 108;
vmax = 2.2;
hmax = 62;
m0 = 450;
mmin = 158;
a = t/tmax*(m0 - mmin)/mmin + 1;
v = a*t;
vtemp = v /. {t -> tmax};
v = a*t*vmax/vtemp;
Lkm = Integrate[v, t];
Lkmtemp = Lkm /. {t -> tmax};
hkm = Lkm*hmax/Lkmtemp;
t0 = Range[tmax + 1] - 1;
ht = hkm /. {t -> t0} // N;
vt = v /. {t -> t0} // N;
vtkmph = Round[vt*60*60];
h2af35table = Prepend[Transpose[{t0, ht, vt, vtkmph}],
{"経過秒", "高度km", "速度km/s", "速度km/h"}];
Grid[h2af35table, {Alignment -> Left, Dividers -> {All, All}}]

■■ 何秒後に見え始めるか? ■■
射点が見える場所で見学するときは問題ないが、遠隔地だとリフトオフからしばらくは何も見えないので心が非常に焦ることになる。意外とこれが曲者で、欲が出てちょっとレンズの向きを変えてみたくなったりして、いじった瞬間に光が見え始めて撮影失敗という愚かな出来事が実際あった。何年も放置していたこの記事をまとめることにしたきっかけかもしれない。ロケット打ち上げは昼間に行われることが多いが、天候さえ良ければ見える可能性があるのではないかと以前から考えている。条件の厳しい日中に視認するためにはいつ、どこに見えるかを事前に予測して高倍率の双眼鏡などで監視する必要があると思われる。あるいは、IRスコープで燃焼を監視するなどの方法も面白い。とりあえず今後のためにこの問題について考えておきたい。
以下緑色の段落はWolfram言語環境の注釈。今では手が届かない高額なソフトになってしまったMathematicaを無料で使えるとは素晴らしい。
前提条件として計画書に載っている以下の値を使う。
- 以下はH2AF35の値
- SRB燃焼終了時間=108秒
- 到達高度=62km
- その時の速度=2.2km/s
等速運動で上昇するなら比例按分で時刻による高度が決まるが、ロケットの場合燃料消費につれてロケット全体の質量が減少するので、同じ推力だと時間が経つほど加速度は大きくなる。
検討するのは主モータとSRBが燃焼している間なのでこの両端の質量がわかれば加速度の比がわかり、これから2.2km/sに達するまでの速度プロファイル、ひいては62kmに達するまでの高度プロファイルもわかると思われる。
打ち上げの瞬間は垂直でその後ノズルの方向を動かして東向きに変針しているはずだが
ここは単純化してSRB燃焼終了まで素直に直線的に上昇していると仮定する。
ロケットの構成や燃料の質量はWikipediaの「H-IIAロケット」
に載っていたので拾ってみる。
Wikipediaで確認するとH2AF35の場合型式名はH2A204型と呼ばれるもので諸元は以下の通り
全体質量445t
→お客さんである「みちびき3」は含まれないかもしれないので4.7tを加えて総質量450tとする。
SRBの燃料は66t x4本
主モータの燃料は101tだが390秒のうち108秒までに消費するのは101x108/390=28tとしておくと
108秒後には総質量=450-66x4-28=158tとなる。
したがって打ち上げ時と燃焼終了時では加速度の比率は
158:450=1:2.848となる。
時刻をt秒、変化を見るためだけの仮の加速度をatempとするとatempは次のように置ける。
(SRB燃焼中の変化を見るだけなので値は後で係数をかけて調整する)
燃料の消費速度は一定と仮定、またこの間の推力も一定と仮定すると
In[1]:= atemp = t/108*1.848+1
Out[1]= 1+0.0171111 t
速度をvとすると
In[2]:= v = atemp t
Out[2]= (1+0.0171111 t) t
atempは仮の値であり、このままでは終端が2.2km/sにならないので、
今求めたvにt=108を代入した時の速度vtempを求めこれで割って調整することにする。
関数式にパラメータを代入するときは「代入対象/.{変換ルール}」のようにやればよい。In[3]:= vtemp = v /. {t -> 108}
Out[3]= 307.584
In[4]:= v = atemp t*2200/vtemp
Out[4]= 7.15252 (1 + 0.0171111 t) t
調整後の本当の加速度は
In[ ]:= a = D[v,t]//Simplify
Out[ ]= 7.15252 + 0.244775 t
単位をGで表すには9.8m/s2で割って
In[ ]:= g = a/9.8;
確認のためこれらをプロットしてみる。
加速度
In[ ]:= Plot[a, {t, 0, 108},
PlotRange -> {{0, 110}, {0, 40}},
GridLines -> Automatic,
AxesLabel -> {"経過秒", "加速度m/s/s"}]
PlotRange -> {{0, 110}, {0, 40}},
GridLines -> Automatic,
AxesLabel -> {"経過秒", "加速度m/s/s"}]
In[ ]:= Plot[g, {t, 0, 108},
PlotRange -> {{0, 110}, {0, 4}},
GridLines -> Automatic,
AxesLabel -> {"経過秒", "加速度G"}]
PlotRange -> {{0, 110}, {0, 4}},
GridLines -> Automatic,
AxesLabel -> {"経過秒", "加速度G"}]
In[ ]:= Plot[v, {t, 0, 108},
GridLines -> Automatic,
AxesLabel -> {"経過秒", "速度m/s"}]
GridLines -> Automatic,
AxesLabel -> {"経過秒", "速度m/s"}]
移動経路に沿って測った距離km
In[ ]:= Lkm = Integrate[v, t]/1000
Out[ ]= 0.00715252 (0.5 t^2 + 0.0057037 t^3)
In[ ]:= Plot[Lkm, {t, 0, 108},
GridLines -> Automatic,
AxesLabel -> {"経過秒", "移動距離 km"}]
Out[ ]= 0.00715252 (0.5 t^2 + 0.0057037 t^3)
In[ ]:= Plot[Lkm, {t, 0, 108},
GridLines -> Automatic,
AxesLabel -> {"経過秒", "移動距離 km"}]
高度
今欲しいのは高さだけなので108秒間軌道に沿って移動した距離Lkmで割って
打ち上げ計画表の高度62kmにあわせてしまうことにする。
In[ ]:= hkmtemp=Lkm/.{t->108}
Out[ ]= 93.1045
In[ ]:= hkm = 62 Lkm/hkmtemp
Out[ ]= 0.00476299 (0.5 t^2 + 0.0057037 t^3)
In[ ]:= Plot[hkm, {t, 0, 108},
GridLines -> Automatic,
AxesLabel -> {"経過秒", "高度 km"}]
Out[ ]= 93.1045
In[ ]:= hkm = 62 Lkm/hkmtemp
Out[ ]= 0.00476299 (0.5 t^2 + 0.0057037 t^3)
In[ ]:= Plot[hkm, {t, 0, 108},
GridLines -> Automatic,
AxesLabel -> {"経過秒", "高度 km"}]
In[10]:= Solve[{hkm==21,t>0}]
Out[10]= {{t->70.017}}
例えば先に求めた21kmまで上昇するのは打ち上げ後70秒とわかる。
In[11]:= Solve[{hkm==16,t>0}]
Out[11]= {{t->62.605}}
16kmまで上昇するのは打ち上げ後63秒
都度Solveするのは面倒なので数表を作っておこう。
時刻の数列を1秒刻みにt0とすると
In[12]:= t0=Range[109]-1
Out[12]= {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,
22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,
44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,
66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,
88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,
107,108}
これを先ほど求めたhkmに代入する。
In[13]:= ht=0.00476299 (0.5 t^2 + 0.0057037 t^3) /.{t->t0}
Out[13]= {0.,0.00240866,0.00974331,0.022167,0.0398426,0.0629332,
0.0916018,0.126011,0.166325,0.212706,0.265316,0.32432,0.389879,
0.462158,0.541318,0.627524,0.720937,0.821722,0.93004,1.04606,
1.16993,1.30183,1.44191,1.59035,1.74729,1.91291,2.08737,2.27083,
2.46345,2.66541,2.87685,3.09794,3.32885,3.56974,3.82077,4.0821,
4.35391,4.63634,4.92957,5.23375,5.54906,5.87565,6.21368,6.56332,
6.92474,7.29809,7.68354,8.08125,8.49138,8.9141,9.34957,9.79795,
10.2594,10.7341,11.2222,11.7239,12.2393,12.7686,13.3119,13.8694,
14.4414,15.0279,15.629,16.2451,16.8762,17.5225,18.1841,18.8613,
19.5541,20.2628,20.9875,21.7284,22.4856,23.2593,24.0497,24.8568,
25.681,26.5224,27.381,28.2571,29.1509,30.0625,30.992,31.9397,
32.9056,33.89,34.8931,35.9149,36.9556,38.0155,39.0946,40.1932,
41.3113,42.4492,43.6071,44.785,45.9832,47.2018,48.4409,49.7008,
50.9816,52.2835,53.6066,54.951,56.3171,57.7048,59.1144,60.5461,
61.9999}
ついでに速度も
In[14]:= vt=0.00715252 (1 + 0.0171111 t) t /.{t->t0}
Out[14]= {0.,0.00727491,0.0147946,0.022559,0.0305683,0.0388223,
0.0473211,0.0560646,0.065053,0.0742861,0.0837639,0.0934866,
0.103454,0.113666,0.124123,0.134825,0.145772,0.156963,0.168399,
0.18008,0.192005,0.204176,0.216591,0.229251,0.242156,0.255305,
0.268699,0.282339,0.296222,0.310351,0.324724,0.339342,0.354205,
0.369313,0.384666,0.400263,0.416105,0.432192,0.448523,0.4651,
0.481921,0.498987,0.516297,0.533853,0.551653,0.569698,0.587988,
0.606522,0.625302,0.644326,0.663595,0.683108,0.702867,0.72287,
0.743118,0.763611,0.784348,0.805331,0.826558,0.84803,0.869746,
0.891708,0.913914,0.936365,0.95906,0.982001,1.00519,1.02862,
1.05229,1.07621,1.10038,1.12478,1.14944,1.17434,1.19948,1.22487,
1.2505,1.27638,1.3025,1.32887,1.35548,1.38234,1.40944,1.43679,
1.46438,1.49221,1.52029,1.54862,1.57719,1.60601,1.63507,1.66437,
1.69392,1.72371,1.75375,1.78404,1.81456,1.84534,1.87636,1.90762,
1.93913,1.97088,2.00288,2.03512,2.06761,2.10034,2.13331,2.16653,
2.2}
時速km/sもついでに
In[15]:= vtkmph=Round[vt*60*60]
Out[15]= {0,26,53,81,110,140,170,202,234,267,302,337,372,409,447,
485,525,565,606,648,691,735,780,825,872,919,967,1016,1066,1117,
1169,1222,1275,1330,1385,1441,1498,1556,1615,1674,1735,1796,1859,
1922,1986,2051,2117,2183,2251,2320,2389,2459,2530,2602,2675,2749,
2824,2899,2976,3053,3131,3210,3290,3371,3453,3535,3619,3703,3788,
3874,3961,4049,4138,4228,4318,4410,4502,4595,4689,4784,4880,4976,
5074,5172,5272,5372,5473,5575,5678,5782,5886,5992,6098,6205,6314,
6423,6532,6643,6755,6867,6981,7095,7210,7326,7443,7561,7680,7800,
7920}
APL言語みたいでとてもお手軽である。
これらをt0と並べると4行109列のArrayになる。
In[16]:= {t0,ht,vt,vtkmph}
Out[16]= {{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,
21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,
42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,
63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,
84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,
104,105,106,107,108},{0.,0.00240866,0.00974331,0.022167,
0.0398426,0.0629332,0.0916018,0.126011,0.166325,0.212706,
0.265316,0.32432,0.389879,0.462158,0.541318,0.627524,0.720937,
0.821722,0.93004,1.04606,1.16993,1.30183,1.44191,1.59035,1.74729,
1.91291,2.08737,2.27083,2.46345,2.66541,2.87685,3.09794,3.32885,
3.56974,3.82077,4.0821,4.35391,4.63634,4.92957,5.23375,5.54906,
5.87565,6.21368,6.56332,6.92474,7.29809,7.68354,8.08125,8.49138,
8.9141,9.34957,9.79795,10.2594,10.7341,11.2222,11.7239,12.2393,
12.7686,13.3119,13.8694,14.4414,15.0279,15.629,16.2451,16.8762,
17.5225,18.1841,18.8613,19.5541,20.2628,20.9875,21.7284,22.4856,
23.2593,24.0497,24.8568,25.681,26.5224,27.381,28.2571,29.1509,
30.0625,30.992,31.9397,32.9056,33.89,34.8931,35.9149,36.9556,
38.0155,39.0946,40.1932,41.3113,42.4492,43.6071,44.785,45.9832,
47.2018,48.4409,49.7008,50.9816,52.2835,53.6066,54.951,56.3171,
57.7048,59.1144,60.5461,61.9999},{0.,0.00727491,0.0147946,
0.022559,0.0305683,0.0388223,0.0473211,0.0560646,0.065053,
0.0742861,0.0837639,0.0934866,0.103454,0.113666,0.124123,
0.134825,0.145772,0.156963,0.168399,0.18008,0.192005,0.204176,
0.216591,0.229251,0.242156,0.255305,0.268699,0.282339,0.296222,
0.310351,0.324724,0.339342,0.354205,0.369313,0.384666,0.400263,
0.416105,0.432192,0.448523,0.4651,0.481921,0.498987,0.516297,
0.533853,0.551653,0.569698,0.587988,0.606522,0.625302,0.644326,
0.663595,0.683108,0.702867,0.72287,0.743118,0.763611,0.784348,
0.805331,0.826558,0.84803,0.869746,0.891708,0.913914,0.936365,
0.95906,0.982001,1.00519,1.02862,1.05229,1.07621,1.10038,
1.12478,1.14944,1.17434,1.19948,1.22487,1.2505,1.27638,1.3025,
1.32887,1.35548,1.38234,1.40944,1.43679,1.46438,1.49221,1.52029,
1.54862,1.57719,1.60601,1.63507,1.66437,1.69392,1.72371,1.75375,
1.78404,1.81456,1.84534,1.87636,1.90762,1.93913,1.97088,2.00288,
2.03512,2.06761,2.10034,2.13331,2.16653,2.2},{0,26,53,81,110,
140,170,202,234,267,302,337,372,409,447,485,525,565,606,648,691,
735,780,825,872,919,967,1016,1066,1117,1169,1222,1275,1330,1385,
1441,1498,1556,1615,1674,1735,1796,1859,1922,1986,2051,2117,
2183,2251,2320,2389,2459,2530,2602,2675,2749,2824,2899,2976,
3053,3131,3210,3290,3371,3453,3535,3619,3703,3788,3874,3961,
4049,4138,4228,4318,4410,4502,4595,4689,4784,4880,4976,5074,
5172,5272,5372,5473,5575,5678,5782,5886,5992,6098,6205,6314,
6423,6532,6643,6755,6867,6981,7095,7210,7326,7443,7561,7680,
7800,7920}}
Prepend関数でタイトルヘッダ文字列を連結し、転置する。
(結果が長いのでShort関数を使って表示を短くする)
In[17]:= Prepend[Transpose[{t0,ht,vt,vtkmph}],
{"経過秒","高度km","速度km/s","速度km/h"}];
Short[%,10]
Out[17]= {{経過秒,高度km,速度km/s,速度km/h},{0,0.,0.,0},
{1,0.00240866,0.00727491,26},{2,0.00974331,0.0147946,53},
{3,0.022167,0.022559,81},{4,0.0398426,0.0305683,110},
<<98>>,{103,54.951,2.03512,7326},{104,56.3171,2.06761,7443},
{105,57.7048,2.10034,7561},{106,59.1144,2.13331,7680},
{107,60.5461,2.16653,7800},{108,61.9999,2.2,7920}}
枠をつけると数表ができた。
In[18]:= Grid[%,{Alignment->Left,Dividers->{All,All}}]
%というのは直前に評価した結果を表す。
In,Outの数字を使って%nnとすればnn番目の結果を表す。
これはグラフィックスのオブジェクトでも構わない。
入力のあと「;」をつければ結果は表示されない。
以上経過を確認しながら計算してきたが、;で区切りながら
一つのセルに入力しておき、そのセルにフォーカスがある状態で
Shift+Enterを押せば上の表が一発で返ってくることになる。
tmax = 108;
vmax = 2.2;
hmax = 62;
m0 = 450;
mmin = 158;
a = t/tmax*(m0 - mmin)/mmin + 1;
v = a*t;
vtemp = v /. {t -> tmax};
v = a*t*vmax/vtemp;
Lkm = Integrate[v, t];
Lkmtemp = Lkm /. {t -> tmax};
hkm = Lkm*hmax/Lkmtemp;
t0 = Range[tmax + 1] - 1;
ht = hkm /. {t -> t0} // N;
vt = v /. {t -> t0} // N;
vtkmph = Round[vt*60*60];
h2af35table = Prepend[Transpose[{t0, ht, vt, vtkmph}],
{"経過秒", "高度km", "速度km/s", "速度km/h"}];
Grid[h2af35table, {Alignment -> Left, Dividers -> {All, All}}]
なお別記事で仰角についても考察した。
「観測地を与えてロケットの仰角リストを求める。石鎚山、剣山からの見え方も。」
■■ Циолковский ■■
JAXAや三菱重工など中の人によって計算された値が公開されているので当たりをつけることができたが、実際には各種の制限条件の中でパラメータを調整しながら打ち上げ計画を立てているはずである。その基礎になるのがツィオルコフスキーの公式である。
Wikipediaからそのままコピペすると
ロケットの初期の質量を m0、
Wikipediaからそのままコピペすると
ロケットの初期の質量を m0、
時間 T 経過後の質量を mT、
質量変化は推進剤として速度 w で噴射されたものとすると、
時間 T 経過後のロケットの速度変化分 ΔV は次の式で表される(ln は自然対数)。
インターステラテクノロジズの稲川さんが公開している「OpenTsiolkovsky」
https://github.com/istellartech/OpenTsiolkovsky/
https://github.com/istellartech/OpenTsiolkovsky/wiki/input_file
ちゃんとやれば色々出てKMLをだすことも可能になっているようだが
パラメータがわからないので手を出すには至らず...。
という記事がありパラメータを推定(妄想)して計算した例が出ている。
またブログ「OSQZSS」にも
https://blog.goo.ne.jp/osqzss/e/a7a92acc22c285c0f7c455b3867bde8f
にもOpenTsiolkovskyの使用例が出ている。
次に探したくなったときのためのリンク集として置いておく。
インターステラテクノロジズの稲川さんが公開している「OpenTsiolkovsky」
https://github.com/istellartech/OpenTsiolkovsky/
https://github.com/istellartech/OpenTsiolkovsky/wiki/input_file
ちゃんとやれば色々出てKMLをだすことも可能になっているようだが
パラメータがわからないので手を出すには至らず...。
ご本人のブログで「衛星打上げロケットSS-520 4号機の予測(妄想)」
http://www.ina111.org/archives/1161という記事がありパラメータを推定(妄想)して計算した例が出ている。
またブログ「OSQZSS」にも
https://blog.goo.ne.jp/osqzss/e/a7a92acc22c285c0f7c455b3867bde8f
にもOpenTsiolkovskyの使用例が出ている。
次に探したくなったときのためのリンク集として置いておく。
■■ 実践的アプローチ ■■
ここまでは観測地とロケットを結ぶ線上に障害物がないという仮定を置くことで課題を単純化して考えてきたが、これは肝心の点に目をつぶっているに過ぎない。例えば倉敷から南西方向を見ると九州の手前に1500m近くの山がそびえている。車のCMで有名なUFOラインのあたりがちょうど邪魔になる。観測場所によっては標高2000mの石鎚山が障害となることもある。このように現実問題では日本の地表は平らな球面ではなく必ず視界を遮る山がある。Wolfram言語でも標高データ
https://reference.wolframcloud.com/cloudplatform/ref/GeoElevationData.html
やGeoで始まる関数がたくさん提供されておりこちらだけでも色々できると思われる。
https://reference.wolframcloud.com/cloudplatform/tutorial/GeoGraphics.html
チュートリアルを見るだけで興奮するが、ここはいったんレンダリングやモデリングの作業性が良いGoogleEarth(Pro)に戻るのが現実的だろう。
最終的には一般化して軌道の時刻付きKML、観測地の緯度・経度・標高、撮影レンズの画角(焦点距離とセンサーサイズ)を与えて非常に正確な所定時刻の静止画像、またはアニメーションを作成する際にはふたたびWolframCloudに戻ってくることになるだろう。
これまでの検討でリフトオフからの経過秒数と到達高度がだいたいわかったので、軌道のKMLの標高を色分けしておけば山の端から見える最初の色で何秒後から見え始めるかがわかることになる。あるいは軌道KMLとは別に種子島上空に標高を変えながら直線を並べて色を変えておくという手もある。これはGoogleEarthで簡単にできる。
この「空間ものさし」をKMLで保存し、GoogleEarthProに加えて2008年12月に招待制で使えるようになったGoogleEarthStudioに読み込んでレンダリングすればかなり正確でリアルな可視化ができる。
例えば成羽近くの標高550m地点からH2BF5の軌道を見たところ。
色は抵抗素子のカラーコードと同じにしてある。
0 黒
1 茶
2 赤
3 橙
4 黄
5 緑
6 青
7 紫
8 灰
9 白
標高30kmまでを1km刻みにしてあり、一番低いところでかろうじて見えているのが茶色の21kmラインである。少しでも東に移動すると四国山地の石鎚山がじゃまになって見えなくなることがわかる。
射点方位が開けている観測場所の候補についてこのような図を作成し、下見もしておけば
いざという時天候に応じて移動し落ち着いて撮影することができるだろう。
GoogleEarthで作成したKMLをGoogleEarthStudioでに読み込んで動画にしてみた。
https://reference.wolframcloud.com/cloudplatform/ref/GeoElevationData.html
やGeoで始まる関数がたくさん提供されておりこちらだけでも色々できると思われる。
https://reference.wolframcloud.com/cloudplatform/tutorial/GeoGraphics.html
チュートリアルを見るだけで興奮するが、ここはいったんレンダリングやモデリングの作業性が良いGoogleEarth(Pro)に戻るのが現実的だろう。
最終的には一般化して軌道の時刻付きKML、観測地の緯度・経度・標高、撮影レンズの画角(焦点距離とセンサーサイズ)を与えて非常に正確な所定時刻の静止画像、またはアニメーションを作成する際にはふたたびWolframCloudに戻ってくることになるだろう。
これまでの検討でリフトオフからの経過秒数と到達高度がだいたいわかったので、軌道のKMLの標高を色分けしておけば山の端から見える最初の色で何秒後から見え始めるかがわかることになる。あるいは軌道KMLとは別に種子島上空に標高を変えながら直線を並べて色を変えておくという手もある。これはGoogleEarthで簡単にできる。
この「空間ものさし」をKMLで保存し、GoogleEarthProに加えて2008年12月に招待制で使えるようになったGoogleEarthStudioに読み込んでレンダリングすればかなり正確でリアルな可視化ができる。
例えば成羽近くの標高550m地点からH2BF5の軌道を見たところ。
0 黒
1 茶
2 赤
3 橙
4 黄
5 緑
6 青
7 紫
8 灰
9 白
標高30kmまでを1km刻みにしてあり、一番低いところでかろうじて見えているのが茶色の21kmラインである。少しでも東に移動すると四国山地の石鎚山がじゃまになって見えなくなることがわかる。
射点方位が開けている観測場所の候補についてこのような図を作成し、下見もしておけば
いざという時天候に応じて移動し落ち着いて撮影することができるだろう。
GoogleEarthで作成したKMLをGoogleEarthStudioでに読み込んで動画にしてみた。
KMLで空間図形にキャプションを付けるのはちょっとやりづらいので2桁の高度がわかりやすいように2列のカラーコードを作成してみた。これで10kmから69kmまで1km刻みで高度がわかる。
倉敷市連島からこれを見たところ。HFOVは105mmに合わせた。
地上の赤い直線は撮影地と種子島の射点を結ぶ線。
紫の軌道はH2BF5のものなので多少ずれているかも。射点近くはほぼ同じと考えられる。
H2AF41打ち上げ時(2020/02/09)の写真 ノーマルEOS6D 105mm
レベル補正しても何も写っていなかった
天体改造EOS6D+IR850nm 少しレベル補正
可視光域で設計されたレンズのためフォーカスが甘くなっているものと思われる。
手前は地元民にはおなじみ亀島山、その後ろの低い山影は瀬戸内海の対岸、更に後方に四国山地が存在しているがこの日は雲に覆われてスカイラインは一切見えなかった。
射点近くで撮影された方の写真や動画を見ると現地は好天で露点も低かったのだろう。ロケット雲もすぐに消えてしまった感じだった。やはり精密に狙いを定めて長めの望遠で狙う必要があると思われた。
左寄りの低い煙突から出る炎は動画でもよく写っていたのでSRB燃焼点を直接捉える事が可能かもしれない。
ちなみに当日予定していた内海からはこんな感じで見えるはず。石鎚山から外れているので山にかかる雲も避けられ25kmから見え始めることがわかる。今回ここに行けなかったのは残念。なにもないときに一度下見に行っておきたいと思っている。
これはうれしい夜間打ち上げの様子。南が開けた標高450m「霧の海展望の丘」からの撮影。低空に厚い雲があり山の端からの出現にはならなかった。ASI1600MMPro(センサは17.3mm×13.0mm 対角21.9mm)と105mmレンズでSRB分離までがだいたい収まった。SRB燃焼終了後も光は消えておらず、分離しても光りながら落下していることがわかる。フルサイズDSLRなら余裕で収まると思われる。
■■ 天候予測について ■■
岡山からだと岡山だけでなく四国山地の上空の雲が打ち上げ時刻に向かってどうなっていくのかを考える必要がある。無償で利用できる
https://supercweather.com
で雲の状況の予測が確認できるので見通し方向にできるだけ雲がない場所を選定する。
広域・詳細・局地 の解像度があり詳細では予測が出るが無償版のうちは局地については予測は出ない。時間経過とともにどう動くか傾向がわかる点が重要である。
有償契約をすれば「局地」(高解像版)についても予測が表示されるのでありがたい。
JAXAによる射場の紹介
https://supercweather.com
で雲の状況の予測が確認できるので見通し方向にできるだけ雲がない場所を選定する。
広域・詳細・局地 の解像度があり詳細では予測が出るが無償版のうちは局地については予測は出ない。時間経過とともにどう動くか傾向がわかる点が重要である。
有償契約をすれば「局地」(高解像版)についても予測が表示されるのでありがたい。
JAXAによる射場の紹介
https://global.jaxa.jp/about/centers/usc/index.html


















